BCAL reconstruction 01/16/2012

Summary

• too many cluster reconstructed in BCAL (with both algorithms)
• Many of these extra clusters come from poor z-resolution rather than split-off behavior
• z-resolution (= time resolution) is simulated by mcsmear
• poor z-resolution at low energy is due to contribution of dark hits
• davidl plans rewrite of BCAL smearing for greater realism
• results below investigates current state of BCAL smearing code

Procedure

Look at individual DBCALPoint = upstream hit + downstream hit in same BCAL cell, with energy corrected for attenuation, z determined by time difference of the two hits.

Can get "truth" information about how much energy deposited and where from DBCALTruthCell. Since these correspond to SiPM cells, must sum several DBCALTruthCell to correspond with one DBCALPoint.

Compare DBCALPoint with sum of corresponding DBCALTruthCell 's.

This analysis is from a sample of single photon events, with energy uniformly distributed from .05-2.05 GeV, theta uniform from 11-118 degrees. (NOT a uniform distribution in z)

Z resolution

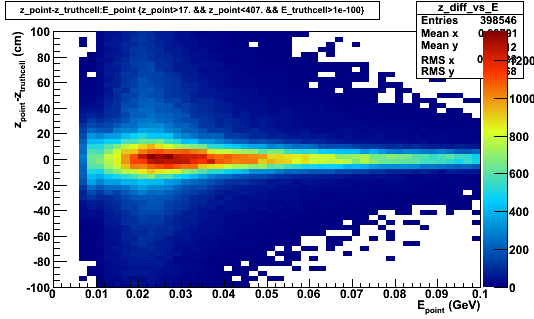
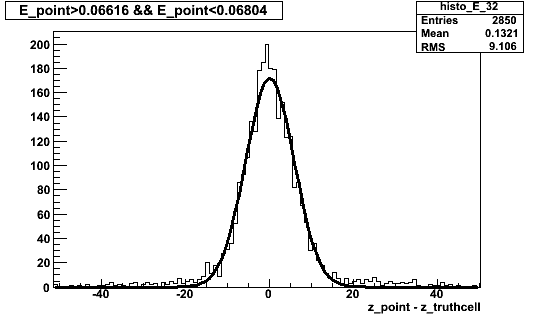
Can look at z-resolution (z_point-z_truthcell) vs E_point:

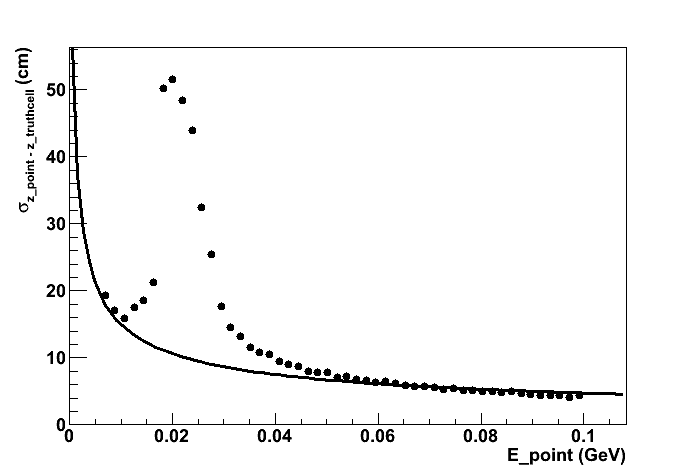
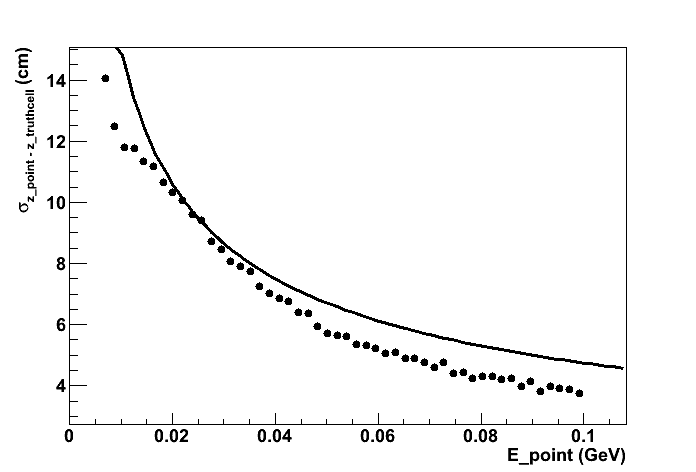
Below are the sigmas of the (z_point-z_truthcell) distributions (fit to a single gaussian) for different slices of E:

The curve shown is 1.5 cm/sqrt(E), which is already higher than the nominal z-position resolution, sigma_z = 1.1 cm/sqrt(E) .

Something strange going on here ???

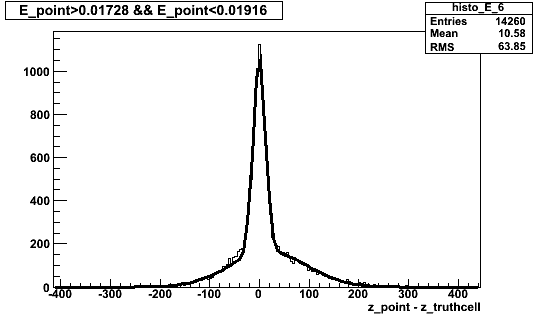
Below is (z_point-z_truthcell) for a range of energies in the anomalous region shown above:

Curve is a fit to a sum of two gaussians. Some points are distributed as expected with a sigma of ~12 cm, but approximately half are distributed with a much large sigma. Why??

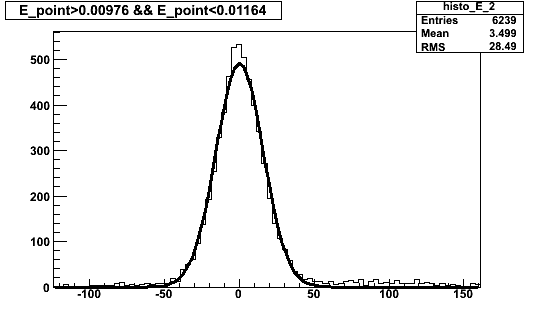
For very small E, and for much larger E, the distribution looks more like a single Gaussian:

small E:

large E:

What's going on

BCAL mcsmear procedure:

1. s_BcalHit_t (->DBCALTruthCell) from hdgeant
2. energy smeared, attenuated to ends
3. end times smeared
4. adjust energy to be consistent with integer # of photoelectrons, add dark hits, smear again due to pedestal
5. at this point s_BcalSiPM*Hit_t (->DBCALSiPMHit) are stored
6. for each fADC cell (upstream and down):
   1. sum up energy from contributing SiPM's, energy-weighted average times
   2. add dark pulses for SiPM's not hit (these also contribute to the energy-weighted average time)
   3. if above threshold, store s_BcalfADC*Hit_t (->DBCALHit->DBCALPoint)
      1. note: thresholds vary by layer

The expected 1/sqrt(E) smearing comes from step 3 above. However, step 6.2 also affects the hit times (and thus the z-position). Since dark hits make up a smaller fraction of large energy hits, there is a larger departure from 1/sqrt(E) behavior at smaller energies. The reason the resolution improves again at very low energy is because these low-energy hits are from layer 1 (layer 1 has the lowest hit threshold), where there is only 1 SiPM per readout cell and thus dark SiPM's, so step 6.2 is skipped.

Disabling dark hits

We can stop mcsmear from add BCAL dark hits by using the -H option.

We can then plot the z-resolution sigmas:

Compare to above. The resolution is much better and not characterized by a large rise at low E.

Effect on clusterization

In certain cases, this poor z-resolution will cause one physical shower to be grouped into two or more clusters.

We can look at the number of BCAL clusters created in b1pi events.

number of BCAL clusters/event: default mcsmear/mcsmear with dark hits disabled

• KLOE algorithm: 6.0/5.0
• GlueX algorithm: 5.7/4.6

The simulation of dark hits (as currently implemented in mcsmear) increases the number of clusters by ~20%.

E distribution

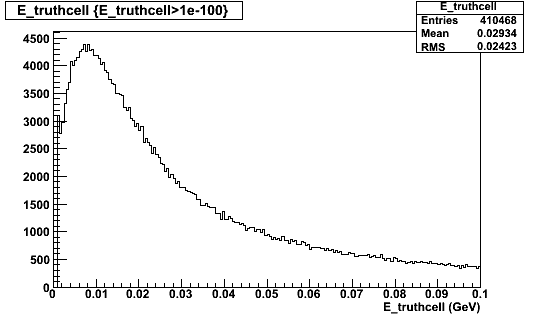
Energy distribution of DBCALTruthCell (after summing to corresponding to readout cells):

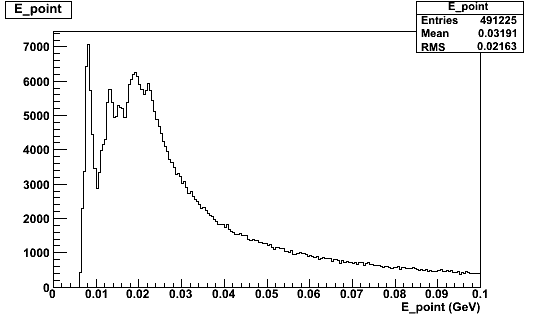
Energy distribution of DBCALPoint :

Where are these peaks coming from? Thresholds?

mcsmear

BCAL mcsmear procedure:

1. s_BcalHit_t (->DBCALTruthCell) from hdgeant
2. energy smeared, attenuated to ends
3. end times smeared
4. adjust energy to be consistent with integer # of photoelectrons, add dark hits, smear again due to pedestal
5. at this point s_BcalSiPM*Hit_t (->DBCALSiPMHit) are stored
6. for each fADC cell (upstream and down):
   1. sum up energy from contributing SiPM's, energy-weighted average times
   2. add dark pulses for SiPM's not hit (these also contribute to the energy-weighted average time)
   3. if above threshold, store s_BcalfADC*Hit_t (->DBCALHit->DBCALPoint)

Thresholds depend on BCAL layer hit:

• BCAL threshold for layer 1: 3.2 MeV (1 SiPMs summed)
• BCAL threshold for layer 2: 5.3 MeV (2 SiPMs summed)
• BCAL threshold for layer 3: 7.3 MeV (3 SiPMs summed)
• BCAL threshold for layer 4: 9.2 MeV (4 SiPMs summed)

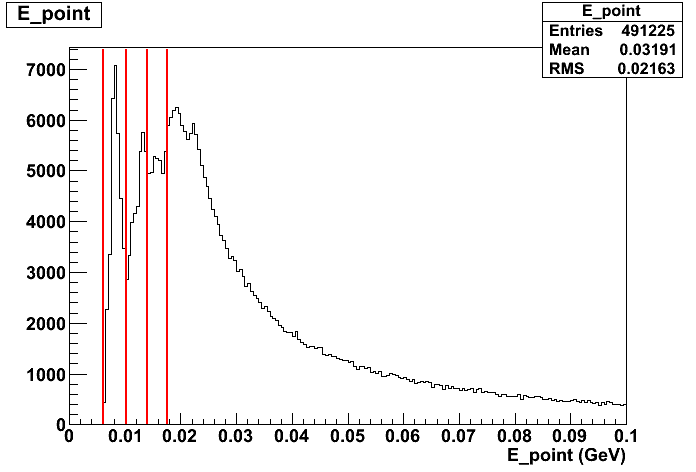
The lowest energy points seen would see 3.2 MeV hits at both ends. We would expect this to result from a hit at the center of the BCAL, which would have an attenuation factor of e^(-(bcal length/2)/(attenuation length))=0.52. So we can calcluate DBCALPoint energies associated with each of the thresholds above (shown as red lines below).

So some of the structure can be explained by thresholds, but not all (it looks like there's an extra peak).

Resolution?

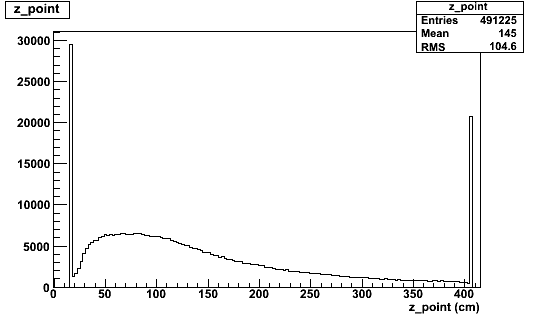
This has to do with points that, when reconstructing z-position from time difference, appear to fall outside the BCAL:

  m_zLocal = 0.5 * cEff * ( tUp - tDown ); 

  // if it is outside the module then set it to the end of the module
  m_zLocal = ( m_zLocal > 0.5 * fibLen ? 0.5 * fibLen : m_zLocal );
  m_zLocal = ( m_zLocal < -0.5 * fibLen ? -0.5 * fibLen : m_zLocal );

This value of z is then used to correct the energy for attenuation.

This leads to a z-distribution like this:

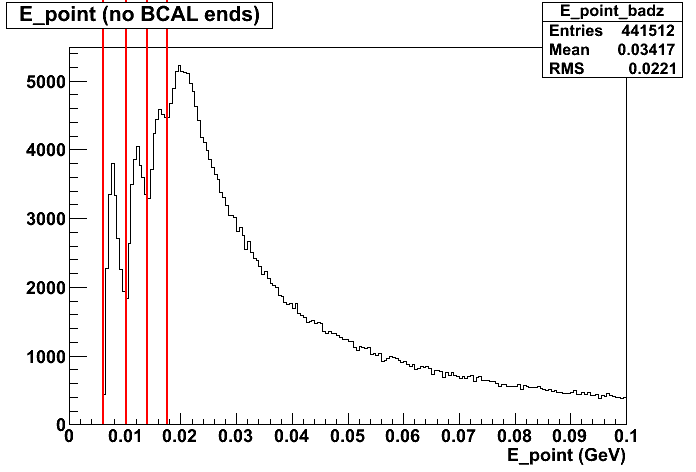
If we ignore the large number of points at z=7 and z=417, the energy spectrum looks as expected:

But the pile-up of points at z=7 and z=417, leads to a lot of attenuation factors of exactly e^(-(bcal length)/(attenuation length)), which when combined with the thresholds, adds in some extra peaks to the spectrum