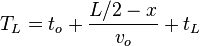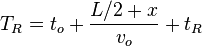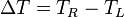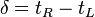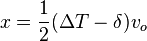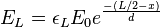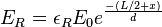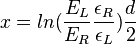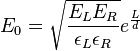ADC data
ADC data: first look
Given that the center of the paddle is x=0 and +x is to the left and -x is to the right we have the following quantities.
- From TDC: with 2*L the length of the paddle,
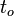 the time of flight of the particle,
the time of flight of the particle, 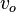 the effective speed of light in the paddle
the effective speed of light in the paddle 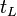 is the internal delay including all cables, PMT transit times ect. and same for
is the internal delay including all cables, PMT transit times ect. and same for 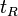
-
- From ADC: with
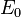 the original energy deposition, d the attenuation length and
the original energy deposition, d the attenuation length and 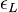 the light transmission through all couplings including the gain of the PMT and attenuation in the cables. The subscripts L and R refer to left and right.
the light transmission through all couplings including the gain of the PMT and attenuation in the cables. The subscripts L and R refer to left and right.
-
- Note, the values
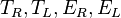 are the measured quantities. And in the following the time measurements are corrected by the relative offsets derived from the calibration procedure. But they have not been corrected for walk. Note also that for all the following plots d=100 is used. Which means the x values
are the measured quantities. And in the following the time measurements are corrected by the relative offsets derived from the calibration procedure. But they have not been corrected for walk. Note also that for all the following plots d=100 is used. Which means the x values
from the adc data will be of by about a factor 2.X where X is around 2.
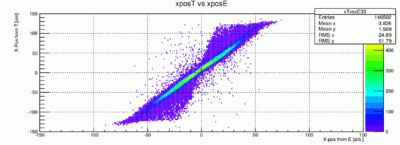
Now we can plot the x information from the TDC against the x information from the ADC:
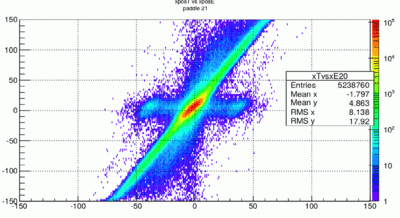
Fitting the slope will result in the attenuation length d with this simple assumption and the horizontal shift is the ration of the two epsilons. You also notice the dip close to x=0. This is due to the fact that ln(1) is zero. We know that the attenuation length is x-dependent and for a better description we need two attenuation lengths. For a central paddle like paddle 21 the distribution is distorted rather strongly. The slopes are quite different in the center and in the tails. Note this is a log plot in z because the center has so much more events. Also in this particular case the TDC x position also seems to be a little off, indicating that the timing calibration for this paddle in this RUN is not yet perfect.
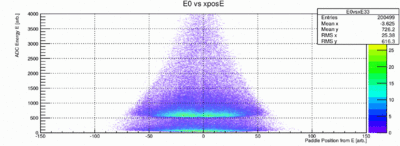
One can also plot the Energy vs. the X-Pos from the ADC data:
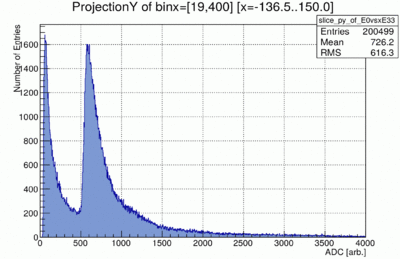
Projecting to the vertical axis or just plot E0 give the histogram below. The location of the peak varies from paddle to paddle.
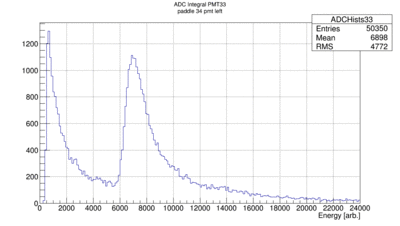
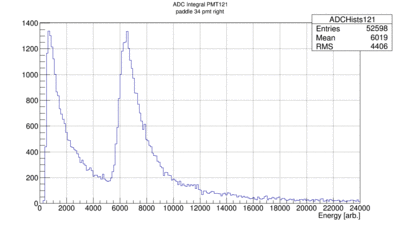
Alternatively the energies 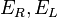 can be plotted separately but requiring that
can be plotted separately but requiring that 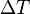 is close to zero meaning that the particle passed though the paddle at or close to the center. In this case both sides see the same amount of light modulo light coupling, detection efficiency and gain. This approach leads to the following two plots:
is close to zero meaning that the particle passed though the paddle at or close to the center. In this case both sides see the same amount of light modulo light coupling, detection efficiency and gain. This approach leads to the following two plots:
What do we want?
- Get a better understanding of the ADC data, the PMT responses.
- Improve on the monitoring the the data quality and the performance of the TOF.
- Procedure (probably iterative) to align all PMT minimum ionizing peaks to the same value. This requires HV changes based on the knowledge of the PMT gains.
- BECAUSE: Having all MPVs a the same value will allow a better adjustment of the common threshold settings in the ADCs and discriminators.
ADC data: Attenuation length
This is an attempt to extract the the attenuation length from the adc data itself.
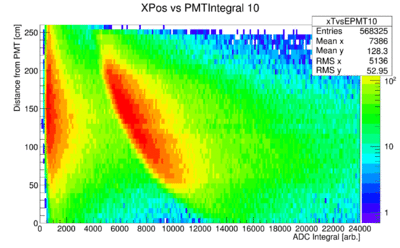
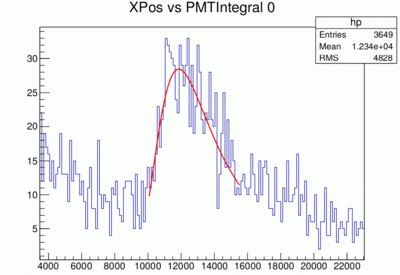
- In a first step we plot the x-position determined from TDC data vs. the ADC integral. An example is shown here for paddle 11 is the pmt ADC integral (horizontal axis) for different x positions along the paddle (vertical axis 40 bins). Note that the z-axis is in log to visualize the low statistic bins in x-position (vertical axis).
- We can then fit each vertical bin (x position) projected to the horizontal axis with a landau convoluted with a Gaussian to find the peak, where in the following example a low statistics histogram is chosen.
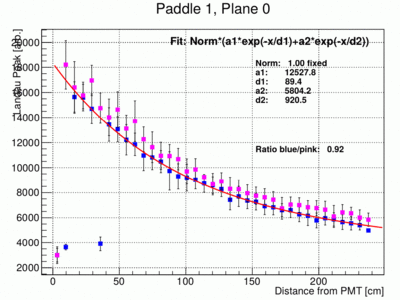
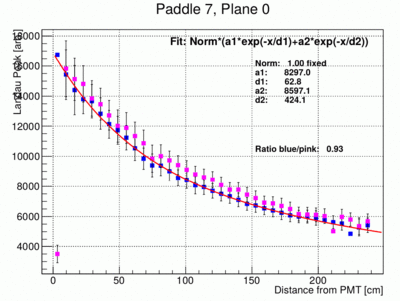
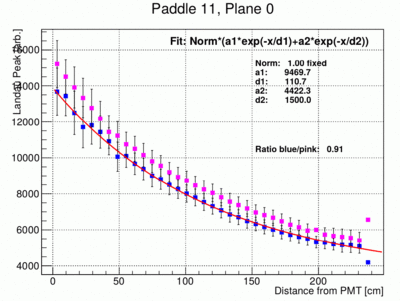
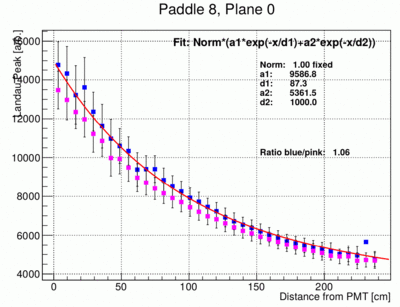
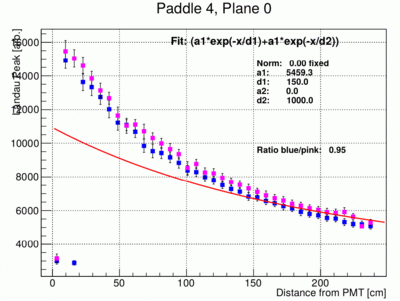
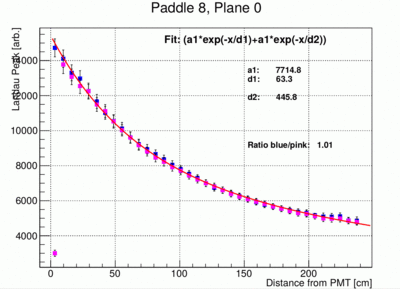
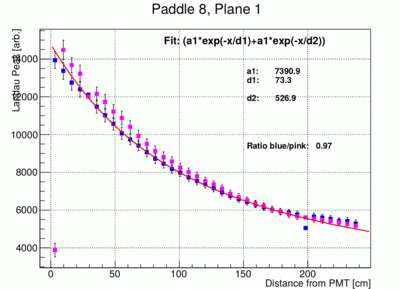
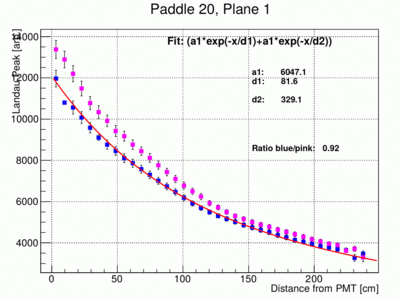
- The peak positions can be plotted as a function of x the distance from the PMT for both ends of each paddle. This is illustrated in the following three plots of the results from paddle 1, 7 and 11. Note that the left and right amplitudes are not the same because of different PMT gains and light collection efficiencies. Before the fit the data for the right PMTs (pink data points) are re-normalized by the factor indicated in the plot (Ration). This normalization factor has been determined using the data points between bin 7 and 30.
- There are several issues with the above results.
- The error bars of the points are basically arbitrary and somewhat overestimated.
- As already done in the above examples the fit parameter Norm is not need and set at 1.
- The fit parameters a1 and a2 are highly correlated. It is probably better to use only one common parameter and set a1=a2
- A major factor for data points being far off from the general trend of the data is the poor control over the landau fit to the initial energy distribution.
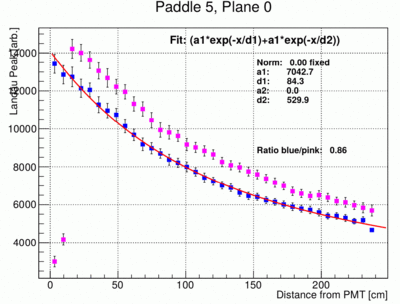
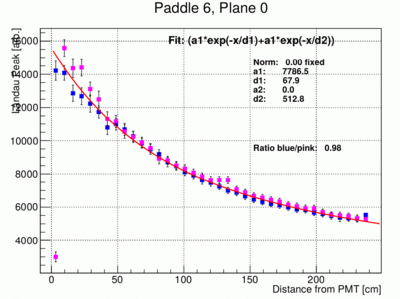
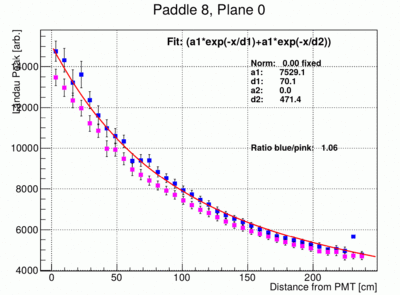
- In the following the fit to the landau peak positions as a function of distance to the PMT is modified to have only 3 free parameters, a1 and two attenuation lengths d1 and d2. The error bars of the individual points have been reduced and are set to FWHM/12 where FWHM is the full width half max of the landau peak. This is of course somewhat arbitrary. The fit result however look much more stable and give much more reproducible results between different paddles. Below the resulting fit for paddle 5, 6, 8 and 4 are shown. Paddle 4 is shown to indicate the fact that sometimes the fit does not find the correct minimum.
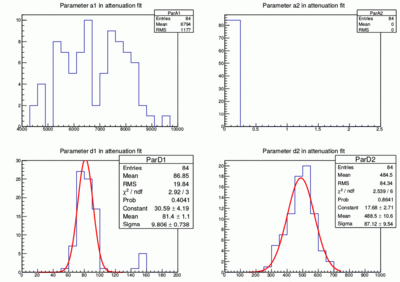
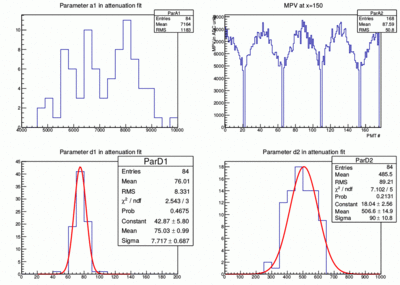
- The results of all paddles for the fit parameters a1, d1 and d2 are shown in the following plot for run 2931. The average attenuation lengths are 81cm and 488cm for d1 and d2 respectively. Using runs 2931, 3079, 3179, 3180 and 3185 together for calibration gives very similar results (second plot).
- In the second plot above the landau peak position is plotted for each pmt. 0-87 are the left/up pmts from plane 0 and plan 1 and 88-175 are the right/down pmts for plane 0 and plane 1. It is clearly seen that the landau peak moves to smaller values the closer the paddles is to the beam hole. The gaps in the plot mark the location of the single ended half length paddles.